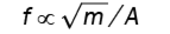Vingeslag på formel
Ved rent teoretiske overvejelser kan man udlede en simpel ligning, der forudsiger, hvor hurtigt en fugl slår med vingerne for at holde sig i luften. Måledata fra flere end 400 flyvende dyr viser, at denne ligning gælder generelt på tværs af arter, kropsstørrelser og flyvestil.
Af Tina Hecksher, Jens Højgaard Jensen og Jeppe Dyre
Når en fugl flyver, så kan hastigheden, hvormed den slår med vingerne, forudsiges af en simpel matematisk ligning. Og det gælder ikke bare fugle, men tilsyneladende alle flyvende dyr – ja, endda også en hval, der slår med halefinnen. Ligningen relaterer vingeslagsfrekvens til kropsmasse og vingeareal, og biologiske data viser, at ligningen gælder uanset dyrets størrelse eller flyvestil.
Dette resultat har vi for nylig publiceret i tidsskriftet PLoS ONE. Andre forskere har gennem tiden også søgt efter universelle mønstre i dyrs flyvning, og både fysikere og biologer er kommet med bud på formler, der beskriver vingefrekvensen. Men disse tidligere forsøg har alle delvist været baseret på empiriske observationer, og ingen har før søgt at generalisere dem på tværs af så mange arter.
En formel bliver til
I vores udledning af formlen, har vi brugt såkaldt dimensionsanalyse. Kort fortalt går det ud på teoretisk at analysere konsekvenserne af, at de to sider på hver side af lighedstegnet i en ligning skal have samme dimension – dvs. de skal repræsentere samme slags fysiske størrelse.
Vores argument var, at vingeslagsfrekvensen er den samme, når en fugl står stille i luften, og når den flyver. For at holde sig svævende i luften skal et stillestående dyr generere en opad-rettet kraft, der balancerer tyngdekraften, og det gør dyret ved at presse luft nedad med sine vinger. Heraf følger, at de størrelser, der betyder noget, må være vingeslagsfrekvensen (hvor hurtigt dyret slår med vingerne), vingearealet (som bestemmer, hvor meget luft, der presses ned per vingeslag), luftens densitet (der bestemmer hvor stor impuls hvert vingeslag genererer) samt forskellige størrelser som former og vinkler, der beskriver det enkelte dyrs vingeform og flyvestil.
Da former og vinkler er dimensionsløse størrelser (dvs. de har ikke en fysisk enhed), slog vi disse størrelser sammen til en enkelt proportionalitetskonstant. De resterende størrelser, dvs. vingefrekvens, vingeareal og luftdensitet, kan kombineres på præcis én måde, der giver en kraft. Ved at antage, at den dimensionsløse proportionalitetskonstant er den samme for alle flyvende dyr og ignorere mindre variationer i lufttæthed og gravitationsfeltstyrke, nåede vi frem til, at vingefrekvensen er proportional med kvadratroden af massen divideret med vingearealet, eller udtrykt formelt:
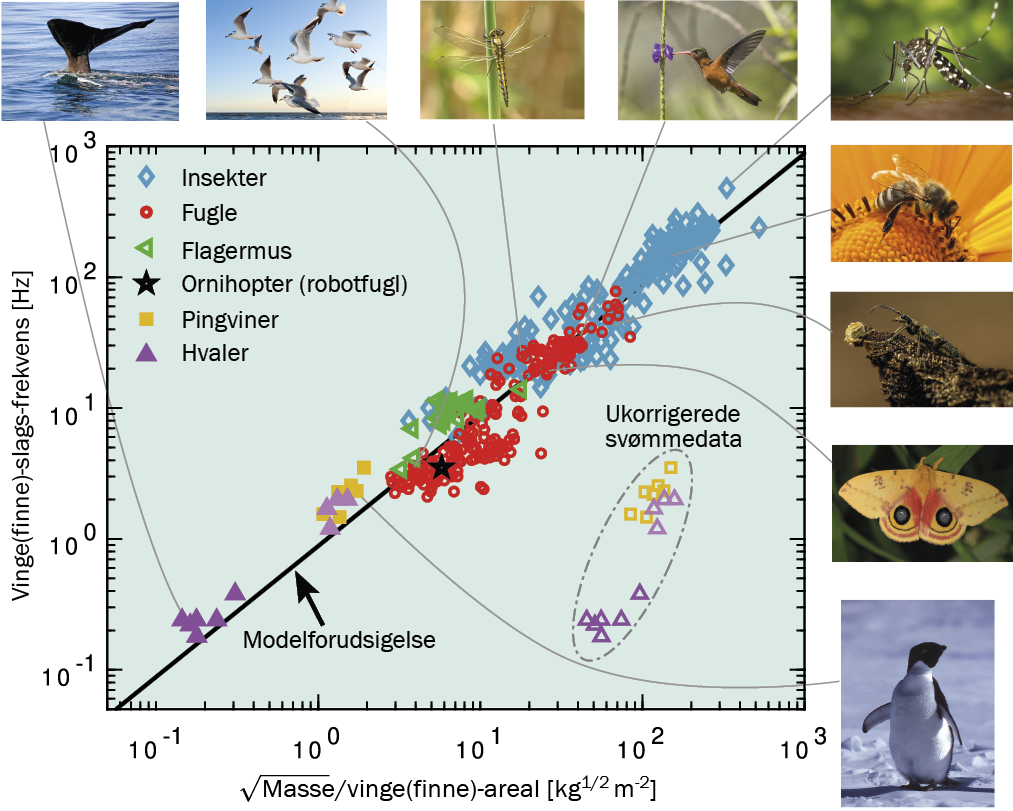
Vores studie var inspireret af et eksamensspørgsmål til et kursus, der går ud på at lære eleverne at “tænke som fysikere”. Eksamensspørgsmålet bad de studerende forklare, hvor hurtigt en fugl skal slå med vingerne for at holde sig svævende i luften – et spørgsmål, man kan nærme sig et svar på ved netop at bruge dimensionsanalyse. Efter eksamen blev vi nysgerrige på, om den udledte formel passede med data.
Formel passer med måledata
For at teste gyldigheden af vores formel indsamlede vi 414 datapunkter fra publicerede undersøgelser, der rapporterer vingeareal, masse og vingeslagsfrekvenser for fugle lige fra svaner til kolibrier, flyvende insekter såsom bier, møl, guldsmede, biller og myg samt flagermus og en enkelt flaksende robot kaldet en ornithopter. Vi inkluderede også data fra hvaler og pingviner. I modsætning til fisk, som bruger luftfyldte blærer til at regulere deres position i vandet, har disse dyr en positiv opdrift og må derfor svømme for at forblive under vandet. Fysikken, der styrer deres finne-frekvens, bør derfor svare til fysikken for vingeslagsfrekvenser, bortset fra en korrektionsfaktor for de forskellige tætheder af luft og vand samt korrektion for opdriften – dyr “vejer” mindre i vand end i luft.
Da vi plottede data for alle dyrene, lå de alle nydeligt på den forudsagte rette linje med lille spredning i datapunkterne. Det betyder, at flyvende dyr på trods af store fysiske forskelle har udviklet sig på en måde, der holder forholdet mellem deres masse, vingeareal og vingeslagsfrekvens relativt konstant.
Umiddelbart var vi overraskede over, at dataene falder på samme linje. For selvom det grundlæggende forhold følger af fysikken, kunne proportionalitetskonstanten i princippet godt være forskellig for forskellige vingeformer og flyvestile.
Man kan undre sig over, at ingen tidligere har afsløret dette simple forhold. Men det kan måske skyldes undersøgelsens tværfaglige karakter. Vores formel er teoretisk udledt baseret på fysikprincipper, og den anviser også, hvordan man skal sammenligne svømmende/dykkende dyr i samme plot som de flyvende dyr. Denne tilgang er mindre almindelig blandt biologer, der ofte arbejder mere empirisk. Det kræver således en kombination af fysik og en stor mængde empiriske data at nå frem til vores resultat. ♦
Tina Hecksher
er lektor i fysik
tihe@ruc.dk
Jens Højgaard Jensen
er lektor emiritus i fysik
Jeppe Dyre
er professor i fysik
Alle ved Roskilde Universitet