
Hvad kan vi regne på en kvantecomputer i dag?
Kvantecomputere eksisterer nu i adskillige laboratorier verden over, men de er stadig langt fra de supercomputere, som teknologien potentielt kan udvikle sig til. Meget tyder på, at de første praktiske anvendelser af kvantecomputere bliver indenfor kemien.
Af Niels Jakob Søe Loft, Emil Bahnsen og Nikolaj T. Zinner
I oktober måned 2019 annoncerede en forskningsgruppe fra Google, at de havde nået en milepæl indenfor kvanteteknologi: De havde fået en kvantecomputer til at slå alle almindelige computere. Det har længe været kendt, at kvantecomputere i teorien kan løse visse opgaver langt mere effektivt end almindelige “klassiske” computere, men at bygge en velfungerende kvantecomputer er en svær opgave. Informationen i en kvantecomputer er lagret som en kvantemekanisk tilstand, og de er notorisk skrøbelige overfor påvirkninger fra omgivelserne. Over tid vil selv de mindste påvirkninger give anledning til tilfældige fejl på resultatet af beregningen.
Forskerne hos Google havde desværre ikke fundet en måde at slippe af med støjen på, men den var tilpas behersket til, at de kunne detektere et statistisk signifikant signal, som de tolkede som et svar fra kvantecomputeren. Beregningen blev udført på en kvantecomputer bestående af 53 kvantemekaniske bits (kvantebits), og forskerne estimerede, at det vil tage de bedste klassiske computere 10.000 år at eftergøre beregningen. Konkurrenten IBM kunne dog siden påvise, at deres klassiske supercomputere kunne udføre opgaven på to og en halv dag. Til trods for det vinder kvantecomputeren dog stadig klart med sine kun 200 sekunders beregningstid.
Selve opgaven, som Googles kvantecomputer har løst, har ingen praktisk anvendelse. Den er designet til at være svær at løse for en klassisk computer, men let for en kvantecomputer, og det er netop den forskel, der er pointen med eksperimentet.
Fordelen ved en kvantecomputer
Når kvantecomputere nævnes i medierne, bliver den tit omtalt som fremtidens vidundermaskine, der kan regne alt på ingen tid og få nutidens supercomputere til at ligne kuglerammer. Det er en sandhed med modifikationer. Det er korrekt, at man har algoritmer til en kvantecomputer, der kan udføre den samme opgave hurtigere end de tilsvarende klassiske algoritmer. Med dette forstår man, at tiden (eller rettere antallet af individuelle beregninger), det tager at udføre kvantealgoritmen, vokser mere favorabelt med opgavens omfang end den bedste klassiske algoritme.
Et ofte fremhævet eksempel er Shors kvantemekaniske algoritme, der kan faktorisere et givet tal i sine primtalsfaktorer. Ethvert naturligt tal kan skrives som et produkt af primtal, eksempelvis 15 = 3 · 5, men at finde primtalsfaktorerne, dvs. at 3 og 5 givet tallet 15, er generelt en hård beregningsopgave. For store tal med hundredevis af cifre er det så svært at finde primtalsfaktorerne, at det udgør låsen i moderne kryptering, der eksempelvis sikrer kommunikationen mellem dig og din netbank.
For sådanne store tal er Shors algoritme langt hurtigere end de bedste kendte klassiske algoritmer for primtalsfaktorisering, og derfor er kvantecomputere blevet set som en trussel mod it-sikkerheden. Dog er truslen mere teoretisk end reel. For at faktorisere et tal, N, skal det først indlæses på kvantecomputeren, hvilket kræver lige så mange kvantebits, som der er bits i den binære repræsentation af N. For eksempel er tallet 15 i bits givet som 1111, hvilket kræver fire (kvante)bits. Kryptografisk relevante tal behøver flere tusinde kvantebits. Til sammenligning har Googles største kvantecomputer 72 kvantebits.
Kvante- og klassiske beregninger
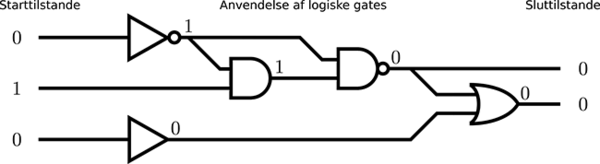
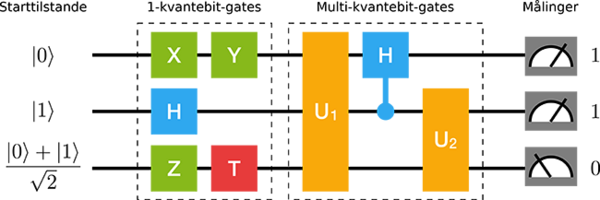
Signal bliver hurtigt til støj
Kan man lave 72 kvantebits, kan man vel også lave tusind? Ja, det er faktisk ingen bedrift at producere en chip med tusinder af superledende kvantebits, der er en af de førende platforme for kvantecomputere, som blandt andet Google og IBM satser på. Udfordringen er at beherske dem. Hver enkelt kvantebit skal manipuleres og kontrolleres gennem ledninger, der transmitterer mikrobølger til og fra kvantebitten, og det kræver godt gammeldags elektronisk udstyr. Elektronikken til at styre bare en håndfuld kvantebits fylder et mindre lokale. Man kan reducere mængden af udstyr ved at opkoble færre kvantebits, men det sker på bekostning af kontrollen over de enkelte kvantebits.
Dernæst er der kvaliteten af de enkelte kvantebits. Sætter man en kvantebit i en bestemt tilstand, for eksempel 0, vil den over tid vekselvirke svagt med sine omgivelser, hvilket efterhånden vil give mere og mere støj på kvantebittens tilstand. Venter man længe nok, er kvantebittens værdi ikke længere 0, men en tilfældig tilstand – altså ren støj. Med andre ord har kvantebits en endelig levetid, før al den information, man har lagret i dem, er gået tabt. Dette sætter en naturlig øvre grænse for beregningstiden, før resultatet går til i støj. Levetiden af superledende kvantebits er typisk 10-100 µs.
Der findes teoretiske metoder til at rette de fejl, der typisk opstår på ens kvantebits, men de bygger typisk på at koble flere kvantebits sammen, hvor nogle af dem bruges til at tjekke og rette fejl. Dermed kommer én kvantebit i computeren til at bestå af adskille fysiske kvantebits på computerchippen. Det komplicerer måden, hvorpå man laver beregninger, og derfor ligger kvanteberegninger med fejl-rettende kvantebits noget ude i fremtiden.
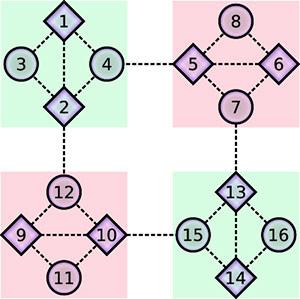
Superledende kvantebits
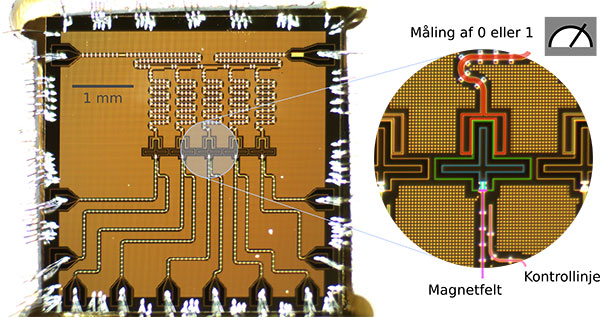
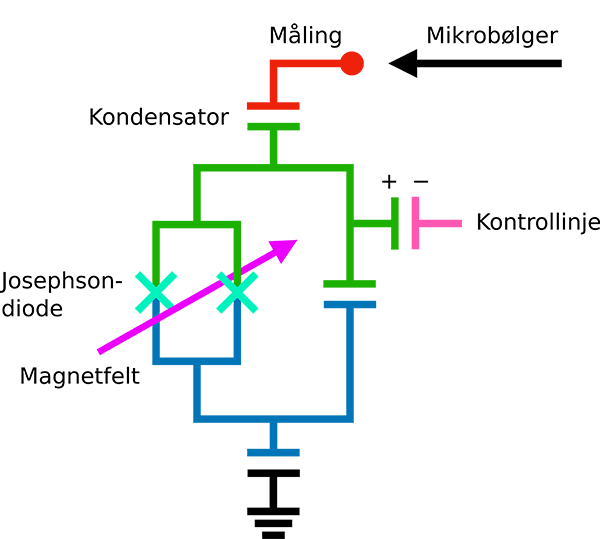

Langt fra brugbare resultater
Når man konkret laver en beregning, dvs. kører en algoritme, udfører man den som en række simple manipulationer af én eller få kvantebits ad gangen. Hver manipulation svarer til en bestemt type operation (kaldet gates), som eksempelvis kan være at ændre 0 til 1 og 1 til 0. I praksis foregår dette på superledende kvantebits ved, at man sender bestemte mikrobølger til sine kvantebits, der påvirker dem til at ændre tilstand.
Kvantemekaniske gates er altså byggeklodserne i alle algoritmer på en kvantecomputer. Det er derfor afgørende, at man kan udføre gates med stor nøjagtighed, især hvis man vil udføre komplicerede beregninger som Shors algoritme, der består af mange gates. På superledende kvantebits kan man i dag lave gates med en nøjagtighed på 99 % eller mere. Det vil med andre ord sige, at gaten forøger støjen på kvantebittene med op til 1 %. Det lyder måske ikke af meget, men fejlene hober sig op: Efter ti gates vil støjen stige til 10 %, og efter 100 gates er næsten 2/3 af informationen tabt.
Denne begrænsning har betydet, at det største tal, man har primtalsfaktoriseret med Shors algoritme på en kvantecomputer er 21 (10101 som binær). Det skete i 2012, da en gruppe brugte fotoner (lyspartikler) som kvantebits. Kvantecomputeren kunne oplyse, at 21 = 3 · 7. Med superledende kvantebits er rekorden 15, som kvantecomputeren faktoriserede i 3 og 5. Det var i øvrigt kun i knap halvdelen af tilfældene, at kvantecomputeren regnede rigtigt.
Kemi på en kvantecomputer
Det ultimative mål er en kvantecomputer med masser af kvantebits, der retter sine egne fejl, og hvor vilkårlige gates kan udføres med tilpas lille fejl på alle kvantebits. En sådan maskine kan blandt andet implementere Shors algoritme og bryde nogle typer kryptering: En vidunder- eller mareridtsmaskine, afhængig af øjnene, der ser. Det bliver ikke lige nu, og heller ikke om lidt. Det interessante spørgsmål er derfor, hvad vi kan gøre med teknologien i dag og indenfor en overskuelig fremtid. Hvad bliver kvantecomputerens første rigtige anvendelse? For at besvare det spørgsmål skal vi finde et anvendelsesområde, hvor det er en naturlig fordel, at computeren følger kvantemekanikkens spilleregler.
Det oplagte svar er at lade kvantecomputeren regne på kvantefysik! Det er ekstremt krævende for klassiske computere at simulere kvantemekaniske systemer, men for en kvantecomputer, der i sig selv er et kvantemekanisk system, er opgaven ligefor. Netop denne fordel ved en kvantemekanisk regnemaskine motiverede forskere som den sovjetiske matematiker Yuri Manin og de amerikanske fysikere Paul Benioff og Richard Feynman til at foreslå idéen om kvantecomputere i starten af 1980’erne.
Specifikt vil man gerne beregne energien af store molekyler, der kan være relevante for medicinalindustrien. Håbet er, at en kvantecomputer indenfor en overskuelig tid kan regne på meget større og komplekse molekyler, end man kan i dag, hvilket kan bane vejen for ny medicin. Energien af et molekyle skyldes et kompliceret kvantemekanisk samspil mellem elektronerne, der arrangerer sig således, at molekylets samlede energi minimeres.
Man kan regne et molekyles energi ud ved hjælp af den såkaldte VQE-algoritme (der står for variational quantum eigensolver), og denne algoritme giver det faktisk mening at køre på nutidens kvantecomputere – alle deres begrænsninger til trods. Kort fortalt er idéen i VQE følgende: I stedet for at køre en række helt specifikke gates på sine kvantebits, vælger man dem delvist tilfældigt. Det er altså ikke afgørende præcis hvilke gates, man udfører på sine kvantebits – i modsætning til for eksempel Shors algoritme, der består af nogle nøje udvalgte gates, der skal udføres med stor nøjagtighed.
Tilfældigheden i VQE-algoritmen gør den fleksibel og modstandsdygtig overfor systematisk støj. Man lader hver kvantebit repræsentere en elektronorbital, og når alle gates er udført, er resultatet en kompliceret kvantebit-tilstand, der svarer til en elektronkonfiguration. Ud fra sluttilstanden kan man regne molekylenergien for den givne konfiguration. Dernæst ændrer (“varierer”) man lidt på valget af gates, hvilket resulterer i en ny sluttilstand med en ny energi. Processen fortsætter, indtil man ikke længere kan sænke energien. På den måde afsøger man forskellige elektronkonfigurationer og finder den, der giver den lavest mulige energi – dette er således elektronerne vil arrangere sig i et virkeligt molekyle.
VQE-algoritmen er allerede blevet brugt til at udregne energien af adskillige molekyler på en rigtig kvantecomputer. Eksempelvis har forskere fra IBM regnet på H2 med to kvantebits, på LiH med fire kvantebits og på BeH2 med seks kvantebits. Det er dog meget simple molekyler, men eksperimenterne viser, at metoden virker.
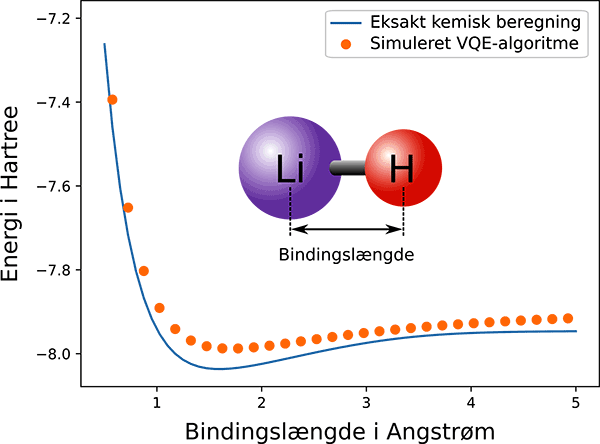
Beregninger af energien af LiH-molekylet (1 Hartree = 4,36 · 10-18 J) som funktion af bindingslængden (1 Angstrøm = 10-10 m). Den blå kurve er resultatet af en kostbar eksakt kemisk beregning, mens de orange punkter er det forventede resultat af en kvanteberegning med VQE-algoritmen på vores fire-kvantebit-computer. Bemærk, hvor tæt VQE-beregningen med blot fire kvantebits kommer på det eksakte resultat.
Nyt design kan spare gates
Præmissen i VQE-algoritmen er, at kvantecomputeren kan producere den kvantebit-tilstand, der svarer til den rigtige elektronkonfiguration. Det afhænger helt af, hvilke gates vi kan udføre. I sidste ende er det betinget af vores hardware og designet af kvantecomputer-chippen.
I vores forskningsgruppe på Aarhus Universitet har vi i samarbejde med internationale kolleger fra blandt andet MIT foreslået et design til en ny gate. Den består af fire superledende kvantebits sammensat i et firkantet diamantmønster, hvorfor vi kalder den “diamantgaten”. Indtil nu har alle gates, der er blevet implementeret på superledende kvantebits, manipuleret enten én eller to kvantebits ad gangen. Til sammenligning manipulerer vores gate alle fire kvantebits på én gang. Det lyder måske ikke af det helt store fremskridt, men det kan faktisk betyde en enorm reduktion i antallet af gates, som man behøver at køre i alt på sin kvantecomputer.
Selvom vores superledende chip endnu ikke er blevet bygget, kan vi godt eksperimentere med diamantgaten. Så længe kvantecomputeren ikke er for stor, kan man godt regne ud på en klassisk computer, hvad den vil gøre i virkeligheden. Vi kan derfor prøve at bruge diamantgaten i en VQE-algoritme og regne ud, hvilket svar en kvantecomputer vil give os tilbage. På den måde har vi set, at én enkelt diamantgate kan regne energien for LiH lige så præcist som IBM kan med tre af deres gates. Det ser altså ud til, at vores gate har nogle nyttige egenskaber og kan bruges til kemiske beregninger med VQE-algoritmen.
Jo større molekylet er, jo flere måder kan elektronerne besætte elektronskallerne på, hvilket kræver flere kvantebits. Vores næste skridt er altså at skalere systemet op, så vi får en kvantecomputer med flere kvantebits. Eksempelvis kan man kopiere diamantgate-konfigurationen fire gange og koble kvantebittene sammen, hvilket giver en 16-kvantebit-computer. Det gør os i stand til at køre diamantgaten på hver af de fire kopier samt at sende information rundt kopierne imellem på en kontrolleret måde. Selvom forøgelsen fra fire til 16 kvantebits ikke lyder voldsom, så eksploderer antallet af forskellige kvantebit-tilstande fra 24 = 16 til 216 = 65.536. I modsætning til en klassisk computer, som kun manipulerer én tilstand ad gangen, kan kvantecomputeren manipulere alle 65.536 tilstande på én gang. Det gør det meget krævende at simulere 16-kvantebit-computeren på vores almindelige computer på kontoret.
Næste stop er en nyttig beregning
Google har vist, at kvantecomputere i praksis kan slå klassiske computere, men har stadig ikke regnet noget interessant ud. Samtidig har VQE-algoritmen vist, at kvantecomputere kan regne molekylenergier ud, men er indtil videre kun demonstreret for små molekyler, hvor vi kender svaret i forvejen. Det næste store mål bliver at kombinere de to ting: At lave et nyttig udregning på en kvantecomputer, som ikke kan udføres på en klassisk computer. Først når dette er sket, har kvantecomputeren for alvor vist sit værd. Det bliver et hårdt kapløb, for det handler ikke kun om prestige, men også om de mange penge, maskinens resultater vil være værd. Løbet er skudt i gang.
