Kryptologi gør beskeder til banken til det rene volapyk
Den moderne, digitale verden ville bryde sammen, hvis det ikke var muligt at sende beskeder til for eksempel banken, advokaten eller bare hinanden, uden at andre kan læse med. Heldigvis sikrer kryptologi, at vi kan kommunikere sikkert på nettet, og bag kryptologien står forholdsvis simpel matematik.
Af Kristian Sjøgren, videnskabsjournalist. ksjoegren@gmail.com
Det er svært at forestille sig et internet uden kryptering. For der kan være rigtig mange gode grunde til, at man ikke har lyst til, at alle kan følge med i, hvad man skriver i fortrolige korrespondancer på nettet. Derfor er det rigtig godt, at matematikere allerede tilbage i 1976 udviklede en matematisk model til at kryptere digitale beskeder. Denne model bliver stadig i dag benyttet overalt på internettet, og derfor kan vi også være ret sikre på, at de beskeder, som kun lægen, banken eller vores nærmeste venner bør læse, ikke bliver læst af andre.
Da internettet så dagens lys tilbage i 1989, havde ingen en idé om, hvor meget denne opfindelse ville omkalfatre hele verdenssamfundet, og hvilke behov det ville stille til blandt andet muligheden for at holde information hemmeligt for andre end dem, som den er tiltænkt. Her skal vi alle være glade for kryptologien, som vi kalder det fagområde, der handler om netop kunsten at kryptere. En af de danske forskere, som har beskæftiget sig mest med kryptologi, er professor Ivan Damgård fra Institut for Datalogi ved Aarhus Universitet.
»Vores verden kunne meget simpelt ikke eksistere, som vi kender den, hvis ikke vi havde mulighed for at kryptere vores beskeder på internettet. Det ville ikke bare betyde, at vi ikke kunne sende beskeder i fortrolighed, men også at alle mine brugernavne og adgangskoder lå frit tilgængelige for alle på nettet. Man er nødt til at have en teknologi, der kan regulere, hvem der kan se hvad, og det er netop det, som kryptologi kan,« forklarer Ivan Damgård.
Alle kan læse dine beskeder
At vi overhovedet har brug for kryptologien skyldes, at computere ikke sender beskeder direkte til hinanden eller til de servere, som de skal kommunikere med. Når du sender en besked til din bankrådgiver, går der med andre ord ikke en lige digital linje fra din computer til din bankrådgivers. I stedet skal din besked forbi alt fra et par til mange hundrede computere, før den når frem. Nettet er nemlig opbygget, så information skal forbi en masse mellemstationer.
Det gør internettet robust, fordi det betyder, at hvis du skal sende en besked til din bank, er du ikke afhængig af, at en forudbestemt sekvens af servere er tændt og fungerer. Din besked finder selv vej via de servere, som er tændt. Omvendt opstår netop det problem, at det er muligt at opsnappe din besked mange forskellige steder, og da internettet er globalt, kan din besked potentielt set bliver opsnappet i både Måløv og Moskva, Kastrup eller Kabul.
»Hvis vi ikke havde kryptologien, ville det at sende en besked til sin netbank være som at sende et postkort, der skulle forbi en hel masse postkontorer rundt om i verden, inden det kom frem til banken. Undervejs ville det være muligt for både postarbejdere og alle mulige andre at læse, hvad du skriver til din bankrådgiver, medmindre beskeden selvfølgelig er af en sådan natur, at kun din bankrådgiver forstår, hvad der står i den,« forklarer Ivan Damgård.
Netop det, at kun din bankrådgiver kan forstå beskeden, er kernen i kryptologi. I overført betydning bruger man kryptologien til at forsyne beskeden med hængelås, som kun en helt specifik nøgle kan låse op, så beskeden kan læses. Det vil sige, at når du sender en besked til din bankrådgiver, sender du en besked afsted med en hængelås, som kun din bankrådgiver har nøglen til. Alle kan stadig tilgå din personfølsomme besked, men hvis de åbner den, står alt skrevet som det rene volapyk.
Primtal er hjørnestenen i kryptologi
Og så skal vi snakke om matematik… Kernen i kryptologien er nemlig forholdsvis simpel matematik, som dog er noget nær umulig at bryde.
For at kryptere en besked og læse den igen, skal man bruge to ting. For det første skal man bruge to primtal, hvilket vil sige tal, som ikke kan fremkomme ved at gange to andre tal med hinanden end tallet selv og 1. Primtallene er 1, 2, 3, 5, 7, 11, 13, 17, 19, 23 osv. osv.
De to primtal ganger man med hinanden, og resultatet er hængelåsen. Det vil sige, at hvis man vil åbne hængelåsen, skal man regne sig frem til, hvad de to primtal, som man ganget med hinanden, har været. Er tallet som eksempel 91, kan du efter lidt forsøg på lommeregneren nok komme frem til, at de to primtal er 7 og 13. Er tallet 391, tager det nok lidt længere tid at finde svaret 17 og 23. De “hængelåse”, som bliver benyttet til at kryptere beskeder på internettet, er på omkring 4000 cifre og er produktet af to primtal på hver omkring 2.000 cifre. Det tager i omegnen af otte millisekunder at gange de to tal sammen. Men det vil omvendt tage millioner af år for selv en supercomputer at regne den anden vej rundt for at finde ud af, hvad de to oprindelige primtal har været.
I praksis foregår det på den måde, at banken fortæller dens kunder, ja faktisk hele verden, at hvis man vil sende en besked til banken, skal den krypteres med det 4.000-cifre store tal. Så er der sat en hængelås på, og så er det kun banken, der ved, hvilke to primtal der skal til for at låse beskeden op igen.
»Bankens hængelås er tilgængelig i offentlige databaser som certifikater, en slags digitalt ID-kort, så man ved, hvordan man kan sende fortrolige beskeder til banken, så kun de kan åbne dem. På en pc kan man se det som et hængelås-ikon i browseren. Det viser, at nu er korrespondance krypteret, og for alle andre end banken vil beskeden være det rene nonsens, for ingen andre end banken keder de to primtal,« siger Ivan Damgård.
Sådan krypterer man en besked
Vi ønsker at kryptere bogstavet “m”. I en computer er alt tal, så bogstavet m repræsenteres af fx tallet 13.
Først vælger vi to primtal, fx 5 og 11, som ganges med hinanden = 55.
Vi krypterer nu beskeden “13” (dvs. “m”) ved at gange tallet 13 med sig selv 3 gange og dividere det med 55. Da 55 ikke går op i 2197 et helt antal gange, får vi en rest, som er 52. Denne rest er nu den krypterede besked. Den matematiske funktion modulo udtrykker netop den rest, man får, når man dividerer et tal med et andet (for eksempel er 11 modulo 4 = 3).
Formelt kan regnestykket altså skrives:
133 modulo 55 = 2197 modulo 55 = 52.
Hvis man kender de to primtal 5 og 11, kan man nemt køre denne proces baglæns og finde frem til beskeden “m”.
At køre processen “baglæns” betyder dog ikke, at man bare kan regne sig tilbage i ovenstående regnestykke. I praksis beregner man en hemmelig nøgle, som er et tal x, der opfylder ligningen:
3x modulo (5-1)(11-1) =1
Her er løsningen x = 27.
Derefter dekrypterer man ved at beregne 52 opløftet til 27 modulo 55, hvilket netop giver 13.
Pointen er, at hvis man ikke kender primtallene (her 5 og 11), kan man slet ikke komme i gang med at løse ligningen med x, fordi man ikke kender tallet (5-1)(11-1).
Computere tænker kun i tal – ikke i bogstaver
Skal vi et spadestik dybere i krypteringen (og matematikken), så krypterer din computer faktisk ikke tekst i dine beskeder til banken, men derimod tal. For en computer findes der nemlig kun tal og ikke bogstaver, så selvom du skriver et “M” i din besked til din bankrådgiver Morten, ser computeren blot tallet 13.
Når beskeden skal krypteres, foregår det typisk på den måde, at tallet, altså 13 for M, bliver ganget med sig selv et antal gange, typisk 3. Derefter dividerer man bankens hængelåstal med tallet, hvilket efterlader en rest. Denne rest er den krypterede besked, som absolut ingen mening giver for nogen som helst. For at få beskeden til at give mening igen, skal man lave hele regnestykket den anden vej, og det kan bare ikke lade sig gøre, medmindre man har adgang til bankens to primtal.
Kommunikationen mellem dig og banken involverer desuden etableringen af en krypteret tunnel mellem din computer og bankens computer, så du ved, at du snakker med banken, fordi du har krypteret din besked med bankens hængelås, og din bankrådgiver ved, at han eller hun snakker med dig, fordi du har brugt et password for at logge på banken.
»Hele dette system til kryptering blev faktisk opfundet inden internettet i slutningen af 1970’erne af forskerne Whitfield Diffie og Martin Hellman og hedder Public-key-kryptering, fordi produktet af primtallene er offentlige (hængelåsen), mens primtallene og altså nøglen til at låse hængelåsen op kun kendes af modtageren af den krypterede besked,« fortæller Ivan Damgård.
End ikke kvantecomputere kan løse krypteringen
Hvis man skal finde ud af, hvilke primtal, der ganget sammen, giver bankens hængelås, går det ikke bare at prøve sig frem. Det ville tage meget længere tid end at prøve samtlige atomer i universet ét for et.
»Det gør det svært at forestille sig, at det kan lade sig gøre. Der findes dog smartere metoder, så man kan komme lidt tættere på at finde tallene, men selv med de bedste metoder, vi kender til, vil det stadig tage millioner af år at bryde krypteringen,« forklarer Ivan Damgård.
Og selvom et eller andet matematikgeni engang skulle finde på en endnu smartere måde at pille tal fra hinanden i primfaktorer, bryder verden ikke sammen af den grund. Kryptering med primtal er nemlig blot én af flere metoder til at kryptere beskeder, så vi kan altid skifte til noget andet, hvis det skulle blive nødvendigt.
Lad os også slå fast, at selvom der har været talt om, at kvantecomputere skulle kunne knække alle mulige krypteringskoder, er der heller ikke her grund til bekymring. Det er godt nok rigtigt, at kvantecomputere – i teorien – kan bryde mange af de krypteringsmetoder, vi bruger på nettet i dag. Men for det første findes der i dag ingen kvantecomputere, som er store nok til at være en trussel i praksis. Det er heller ikke til at sige, om tilstrækkeligt store kvantecomputere kommer til at eksistere inden for de næste 20 eller 50 år – eller nogensinde.
»Men skulle det komme så vidt, så findes der allerede standardiserede nye krypteringsmetoder, som kvantecomputere ikke kan bryde – såkaldt ”postquantum secure”-kryptering,« forklarer Ivan Damgård.
Sådan fungerer MitID
Når det gælder vores færden på internettet, har vi også i andre sammenhænge brug for kryptering. Det kan dreje sig om, at vi skal overføre 65.000 kr. til en mand i Thy for en handel vedrørende en gammel campervan, som var sat til salg på Den Blå Avis. For 20 år siden gik vi i banken og skrev under på overførslen, og så var vores underskrift beviset på, at vi havde sagt god for overførslen. I dag har de færreste af os vores daglige gang i banken, og vi klarer det hele digitalt med blandt andet MitID *Swipe*.
MitID fungerer også efter nogle af de samme principper for kryptering som ved kryptering af beskeder. Her gælder det bare, at når banken skal have bekræftet, at den skal overføre 65.000 kr. til Hans Hansen for køb af en gammel campervan, skal den lige sikre sig, at det rent faktisk er dig, som bestiller overførelsen.
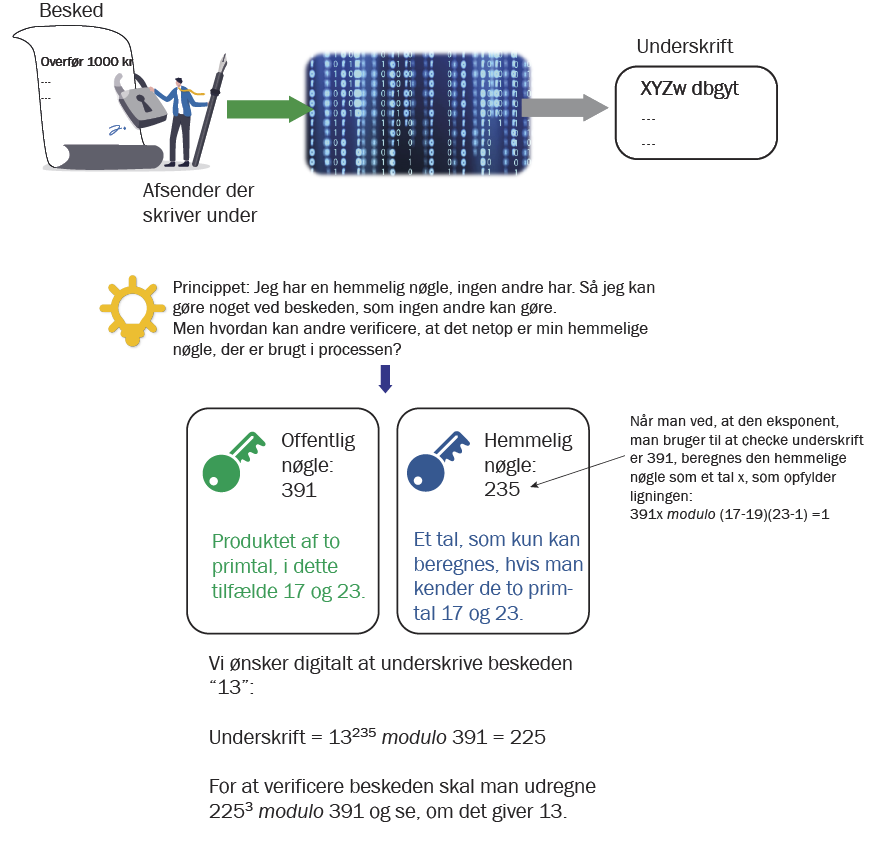
Ved en digital signatur har vi alle sammen en personlig nøgle, som ingen andre har, og det betyder, at kun vi hver især kan gøre noget ved en besked, for at banken kan forstå den eller agere på den. Denne personlige og hemmelige nøgle er igen baseret på relativt simpel matematik, hvor vi tager beskeden, der igen kun består af tal, og ganger tallene med det tal, som er den personlige nøgle. Det kan som eksempel være, at man opløfter beskeden i 14. potens (det reelle tal er meget, meget, meget højere), og kun derved kan banken bekræfte, at beskeden er behandlet digitalt på en måde, som kun personen med den nødvendige nøgle kan have gjort.
»Det gør det muligt at skrive under på ting digitalt og godkende overførsler af penge. MitID er et system, hvor vi alle har en hemmelig signaturnøgle, som opbevares på en central server. MitID er adgangskontrollen til de hemmelige digitale nøgler, så det kun er mig, som gennem mit MitID, min brugerprofil og mit password eller ansigtsgenkendelse kan bruge min digitale nøgle til at underskrive et dokument.
Vi bruger også MitID til at logge på hos Skat, så når jeg logger på Skat, bliver der lavet et lille digitalt dokument, hvor der står, at Ivan i dag på dette og dette tidspunkt forsøgte at logge ind på Skats hjemmeside. Da det er underskrevet med min personlige nøgle, kan Skats hjemmeside tjekke, at det er rigtigt, at det er Ivan, som vil ind, og de kan så lukke mig ind. Det er den måde, som det fungerer på,« siger Ivan Damgård.
Uden matematikken bag kryptering ville det være helt umuligt at forestille sig, at hverken Ivan, dig eller mig kunne sende en besked til banken vedrørende en overførsel af penge, eller at banken overhovedet kunne verificere, hvem der bestilte overførslen.
»Så ville verden bryde sammen og holde op med at eksistere, som vi kender den i dag,« siger Ivan Damgård. ♦
Blockchain er ikke bare Bitcoins
Meget af det, vi foretager os på internettet i dag, er isoleret til digitale “siloer”, der ikke nødvendigvis kommunikerer med hinanden. Skal man som eksempel købe et hus, er banken én silo, og Det Digitale Tinglysningssystem er en anden silo. De to siloer er ikke forbundet, så hvis du køber et hus, skal banken først indhente information fra Det Digitale Tingslysningssystem om, at skødet på et hus er overdraget, før banken overfører pengene fra køber til sælger, og ejerskabet over et hus kan overgå fra én person til en anden. Derudover skal også forsikringen ind over, og det skal RKI og en hel masse andre systemer også. Det tager tid og er alt andet mere besværligt, end det måske burde være.
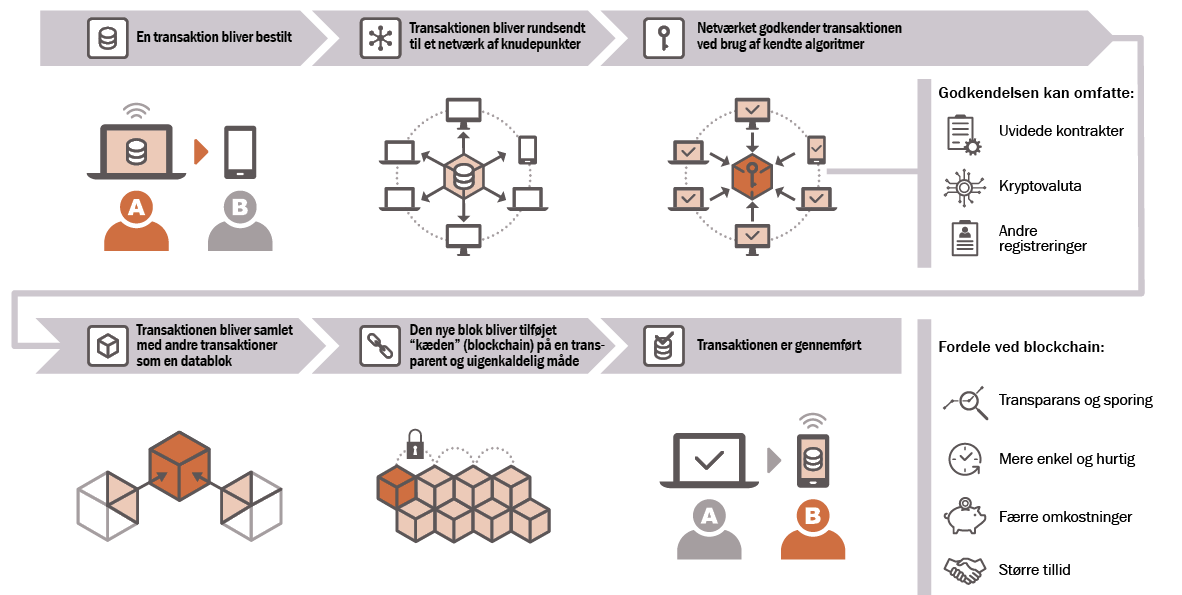
Man kan sige, at blockchain er et opgør med de digitale siloer. Tanken bag blockchain er, at vi alle sammen ”skriver på hver vores digitale opslagstavle”, og at vi er enige om, at det, som står på opslagstavlerne, er rigtigt. Det vil sige, at hvis jeg, banken eller Det Digitale Tingslysningssystem skriver noget på hver vores opslagstavle, kan det ikke tages tilbage igen. Det er blevet en del af den fælles sandhed.
Står der for eksempel på opslagstavlerne, at du ejer et givent hus, vil det ikke være muligt at tage ejerskabet fra dig ved at manipulere med data ét sted i systemet, idet dit ejerskab over huset vil fremgå af alle de andre opslagstavler. Man kan med andre ord se, at nogen har forsøgt at manipulere med tingene. Hvis man endelig forestiller sig, at man vil franarre dig ejerskabet over huset, skal man rette ejerskabet på alle opslagstavlerne samtidig, og det vil kræve, at man ændrer på ejerskabet ved ikke bare at bryde ind i Det Digitale Tingslysningssystem, men at man ændrer i ejerskabsinformationen på tusindvis eller endda millioner af opslagstavler.
Fordelen ved at have et blockchain-system ind over alt det, som vi foretager os på nettet er, at man på opslagstavlerne også kan skrive programmer. Og man kan bestemme, at når visse betingelser er opfyldt, så vil de instruktioner, der står i programmerne, blive udført. Det vil sige, at man som eksempel kan skrive, at så snart jeg har modtaget nøglerne til dit hus, overfører jeg købesummen til dig. Det forpligter jeg mig til, og jeg kan ikke løbe fra den forpligtelse, fordi den er skrevet ud på et hav af digitale opslagstavler, som jeg ikke kan ændre på igen. I stedet for at det ene system skal spørge det andet system, og vi skal vente tre arbejdsdage og en kommunal frokost på, at der sker noget, kan ejerskabet af huset skifte hænder med det samme, fordi alle systemerne blot kan konsultere den fælles sandhed.
Blockchain vil på den måde gøre det muligt at automatisere en hel masse processer, uden at det er muligt at manipulere ved systemet eller lægge det ned.
Blockchain er også den teknologi, som ligger bag Bitcoins som digital valuta. Også her er der digital konsensus om, hvem der ejer de forskellige bitcoins, og det er som sådan ikke muligt for en kriminel at gå ind og stjæle dem ved at overføre ejerskabet over en håndfuld bitcoins til sig selv. Det vil stadig stå på alle de andre opslagstavler, hvem der rigtig ejer de digitale mønter.