Entropiens mysterium
At tiden har en retning, opfatter vi alle som indlysende. Denne sandhed udtrykkes ved den fundamentale naturlov, at entropien i et lukket system kun kan stige eller være konstant. Men hvad ligger der egentlig bag begrebet entropi, og er det 100% korrekt, at entropien aldrig kan aftage?
Af Trond Ingebrigtsen og Jeppe Dyre
Dyr, planter, mennesker – alle ældes de og ender med at dø. Det samme gælder for en stjerne, som “fødes” ud af en stor gas-sky og ender sine dage, når den er brændt ud, som regel efter nogle milliarder år (men hurtigere for tunge stjerner). Dette er alt sammen velkendt. I fag som biologi og geologi er tidsudvikling et helt centralt begreb, hvad enten man taler om en celles eller et individs livscyklus, skabelsen af bjerge og geologiske aflejringer, eller evolutionen i det hele taget. Det, at tiden kun kan gå én vej, kaldes irreversibilitet. Omvendt er en reversibel proces et forløb, som godt kan gå baglæns. Selvom nogle processer er reversible, så kan der ikke være tvivl om, at Verden som sådan er irreversibel.
Ellers ville vi en gang imellem opleve at døde dyr kom til live og blev yngre med tiden for at ende med at blive født.
Hvad er så mysteriet? Det er, at fysikkens helt grundlæggende naturlove alle er reversible. Det gælder, hvad enten vi taler om mekanikkens grundligninger (opstillet af Newton i 1680’erne), elektromagnetismens grundligninger (opstillet af Maxwell i 1860’erne) eller kvantemekanikken, som blev udviklet af en række fremragende fysikere i løbet af 1920’erne.
Vi kender det godt fra hverdagen: Tænk på et pendul, som er sat til at svinge frem og tilbage. Her har tiden ingen retning – om pendulet svinger “forlæns” eller “baglæns” kan ikke afgøres. Hvis man filmede pendulet og viste filmen baglæns, ville man ikke kunne se forskel. Pendulet er altså reversibelt. Dette afspejler, at Newtons anden lov, som beskriver bevægelsen, er reversibel.
Og dog. Vi ved jo alle, at pendulet efterhånden går i stå, så tiden har altså en retning. Vi ved også, hvorfor pendulet går i stå. Det er fordi, der er gnidningsmodstand, som langsomt og løbende omdanner pendulets mekaniske energi til varme. Energien forsvinder ikke, for varme er en energiform. Det, der sker, er, at atomerne i pendulophænget (og i luften) kommer til at bevæge sig lidt hurtigere i takt med, at pendulet går i stå.
Entropien stiger, siger man. Einstein kunne angiveligt forestille sig, at alle naturlove eventuelt må justeres, efterhånden som forskerne bliver klogere, ligesom han selv modificerede Newtons gravitationslov. Bortset fra loven om, at entropien aldrig kan aftage for et isoleret system (det vil sige et, som ikke vekselvirker med sine omgivelser). Denne lov må stå uforandret til evig tid, mente han: Det er umuligt at forestille sig, at entropien kan aftage for et makroskopisk system.

Entropi og sandhed
Ovenstående er ikke bare snak – entropi er en veldefineret størrelse, der kan bestemmes ved hjælp af eksperimenter ligesom for eksempel vægten af en ting. Står du med et glas vand i hånden, har vandet en bestemt entropi. Opvarmes vandet, stiger entropien. Disse erkendelser har været en grundlæggende del af fysikken og kemien siden anden halvdel af 1800-tallet.
Utallige eksperimenter har bekræftet, at entropien aldrig falder for et isoleret system. Blander man 1 liter koldt vand med 1 liter varmt vand, fås 2 liter lunkent vand. Det ved vi alle, men de færreste tænker på, at universets entropi herved stiger og aldrig kommer tilbage til, hvad den var. Vandblanding er en irreversibel proces, for man har aldrig oplevet, at 2 liter lunkent vand pludselig opdeler sig i koldt vand til venstre og varmt vand til højre. Et andet eksempel er, hvis du taber et glas, og det går i stykker. Man har aldrig observeret, at stumperne spontant samler sig, og glasset hopper tilbage i hånden, selvom det ikke i sig selv ville være i modstrid med loven om energiens bevarelse.
Hvordan kan det være, at entropien aldrig kan aftage, når atomers og molekylers opførsel er styret af naturlove, hvor tiden lige så godt kan gå baglæns som forlæns? Nu bliver det lidt filosofisk, for her er det nyttigt at skelne mellem to forskellige sandhedsbegreber: ontologiske sandheder og pragmatiske sandheder.
En ontologisk sandhed er udsagn, som umuligt kan være forkert. For eksempel kan man ikke forestille sig en verden, hvor 3 gange 4 er 13. En pragmatisk sandhed er en erkendelse, som er rigtig for alle praktiske formål, for eksempel at man ikke overlever, hvis man falder ud af en flyvemaskine i 8 kilometers højde. Det er en interessant diskussion, om eksempelvis kvantemekanikkens grundligning er en ontologisk eller en pragmatisk sandhed. Men de fleste fysikere er enige om, at paradokset om entropiens vækst, der trodser de underliggende loves reversibilitet, skyldes, at denne lov ikke er en ontologisk sandhed. Med andre ord: Entropien kan godt aftage. Det er ikke principielt umuligt, men bare helt enormt usandsynligt. At glasset, som er tabt på gulvet, samler sig og hopper tilbage i hånden kan godt ske, men det er bare så usandsynligt, at det aldrig er observeret – og heller aldrig vil blive det, selv ikke i løbet af mange milliarder år.
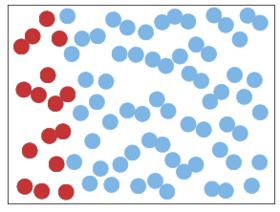
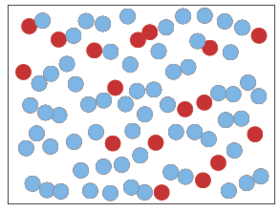
Figur 1. Luft består af cirka 20 % oxygen- (røde) og cirka 80 % nitrogen-molekyler (blå). Den første figur viser en tænkt situation med oxygen og nitrogen adskilte. Med tiden vil molekylerne uvægerligt blandes, og man havner i situationen til højre. Dette er en irreversibel proces, for man vil i praksis aldrig se det modsatte ske, altså at en blanding spontant “ordner sig”. Det er ikke principielt umuligt, men enormt usandsynligt. Entropien er mindre til venstre end til højre, hvor der er mere uorden.
Et spørgsmål om orden
Lad os tage et andet eksempel. Luft består som bekendt primært af cirka 80 % nitrogen (kvælstof) og 20 % oxygen (ilt), som begge er to-atomige molekyler. Hvis man har en beholder med oxygen og nitrogen i hver sin ende adskilt af en væg, som man derefter fjerner, vil alle molekylerne bevæge sig tilfældigt rundt mellem hinanden. Efter kort tid havner man i en situation, hvor oxygen og nitrogen er blandet (figur 1).
Entropien er herved blevet større, og man kan endda beregne, hvor meget den er vokset. Pointen er nu, at man i praksis aldrig ser det modsatte ske. I princippet kunne det ske, at din næste vejrtrækning kun trak nitrogen-molekyler ned i lungerne – hvilket straks ville kunne mærkes! – i praksis sker det aldrig. Det er langt mere usandsynligt end for eksempel at vinde 10 milliongevinster i Lotto 10 uger i træk.
Som sagt er de fleste fysikere enige om ovennævnte forklaring. Men den er dog ikke mere oplagt end, at emnet stadig diskuteres. For eksempel har nobelpristagerne Ilya Prigogine (kemi) og Roger Penrose (fysik) begge givet udtryk for tvivl om denne forklaring på, hvorfor verden er irreversibel, er fuldt ud dækkende.
Ser vi igen på eksemplet med blanding af nitrogen og oxygen, illustrerer det, hvad man sædvanligvis siger, nemlig at entropi er et mål for uorden. Jo større uorden, jo større entropi. Hvis man kaster brikkerne til et puslespil op i luften, skulle det være mærkeligt, hvis de lander, så puslespillet er lagt, for uorden er meget mere sandsynlig end orden. Det er derfor, entropien stiger med tiden. Dette er den gængse forklaring, og den er vi enige i. Man skal dog være skarp på at definere “uorden”.
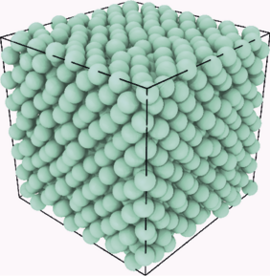
Således kan et system af runde partikler pakkes sammen i en terning ved samme tæthed på forskellige måder, sådan at det system, der umiddelbart ser mest ordnet ud, i virkeligheden er det mest uordnede i den fysisk-kemiske forstand, der definerer entropi (se figur 2).
Figur 2. Figuren til venstre viser en såkaldt “random close packing” af kugler. Kuglerne rører hinanden, så de ikke kan bevæge sig og systemet kan derfor ikke trykkes yderligere sammen. Til højre er kuglerne sat op i et krystalgitter (en såkaldt fladecentreret krystal) i det samme volumen. Selvom denne situation fremtræder mere ordnet end den til venstre, er entropien her faktisk større, fordi kuglerne har plads til at rasle lidt mellem hinanden. Eksemplet viser, at man skal være forsigtig med udsagnet: “Entropi er et mål for uorden”.
Svært at bestemme entropi i en simulering
Ethvert system har en entropi, og for alle praktiske formål kan entropien ikke falde, medmindre systemet vekselvirker med omgivelserne, som når man for eksempel putter “systemet” i et køleskab, hvorved entropien falder.
Noget, der så kan undre én – og som har relevans for vores egen forskning – er, hvorfor det skal være så svært at bestemme entropien i en computer-simulering. I en simulering kender man alle molekylers positioner og hastigheder, som fremskrives løbende ved brug af Newtons love. Man har fuld information om systemet i en sådan simulering. Til hver en tid kan man bestemme systemets energi, dets temperatur, tryk, varmeledningsevne, viskositet (hvis det er en væske), hvordan neutroner vil spredes på systemet, osv. Alt, hvad man kan finde på at spørge om, har man information til at kunne besvare.
Bortset fra entropien!
Selvom man kender alle molekylers positioner og hastigheder til et givet tidspunkt, kan man ikke bestemme entropien herudfra. Det er ikke en gang muligt at få et groft overslag over, hvor stor entropien er. Hvordan kan man have fuldt kendskab til alle positioner og hastigheder og så alligevel ikke kunne beregne entropien herudfra? Kender systemet overhovedet sin egen entropi? Det er da mærkeligt.
En mulig løsning er, at entropi er et begreb, som er mere subjektivt end for eksempel energibegrebet. Altså at entropien afhænger af, hvilke spørgsmål iagttageren stiller til systemet. Dette er synspunktet, som informations-teorien indtager, en teori, som blev udviklet af matematikeren Claude Shannon i løbet af 1940’erne, hvori entropi-begrebet er centralt.
Men hvis entropi er subjektiv, hvad så med den sædvanlige entropi i fysikken og kemien – er den også mere ”in the mind of the spectator” end den eksisterer i virkeligheden? Og hvis det er tilfældet, hvordan kan man så være sikker på, at entropien altid stiger med tiden? Afhænger det også af iagttageren?
Glas og Tid centrets computere, som siden 2008 primært har været baseret på grafikkort. Disse såkaldte GPU-kort regner meget hurtigt, men har den udfordring at de er svære at programmere optimalt, fordi der kræves særlige instruktioner for at udnytte den enorme regnekraft (se http://rumd.org). I dag råder Glas og Tid over en regnekapacitet på godt 1000 TeraFlop.
Hvordan definerer man egentlig entropi?
Vi har ikke skråsikre svar på disse spørgsmål. Måske er det på sin plads her at nævne, hvordan man definerer entropi i den såkaldte “statistiske mekanik”, som er standard-pensum ved universiteters fysik- og kemi-studier verden over.
Energien er som bekendt bevaret for et isoleret system. Hvis det betragtede system er i termisk ligevægt, er entropien et mål for, hvor mange mikrotilstande, der har den givne energi – mere præcist er entropien logaritmen til dette antal. Jo flere tilstande, der har samme energi som systemet, jo højere er entropien. Dermed er entropien et udtryk for vores uvidenhed om systemet, når det kommer til størrelsen energi. Men man kan godt definere andre entropi-begreber, hvert med relation til en specifik størrelse – således at entropien altid udtrykker, hvor mange mikrotilstande, der har samme værdi af denne størrelse. Energi spiller imidlertid en særlig rolle. Det skyldes dels, at energien er bevaret i tid, dels at energi er en additiv størrelse (dvs.: har man to systemer, er energien af det hele summen af de to systemers energi). Det er formentlig på grund af disse to egenskaber ved energi, at den sædvanlige entropi er vigtigere end de mange andre entropier, man kan forestille sig.
Vi har i vores forskning faktisk haft brug for et lidt anderledes entropibegreb end det sædvanlige, nemlig ét som kun refererer til den potentielle energi. Husk, at en sten, der kastes gennem luften, har både en kinetisk energi givet ved hastigheden og en potentiel energi givet ved stenens højde over jorden. Generelt har alle atomer og molekyler en potentiel energi, som afhænger af, hvordan de er positioneret i forhold til hinanden (tyngdekraften spiller ingen rolle her og ignoreres i computer-simuleringer af gasser, væsker eller faste stoffer). Den entropi, som kun vedrører den potentielle energi, kaldes “exces-entropi”.
I 1977 opdagede den israelske fysiker Rosenfeld, at denne størrelse bestemmer en væskes relaksationstid, som udtrykker hvor længe væsken er om at komme i ligevægt efter en lille forstyrrelse. Dette er i dag anerkendt som en vigtig opdagelse, selvom der indtil år 2000 stort set ingen interesse var for Rosenfelds idé.
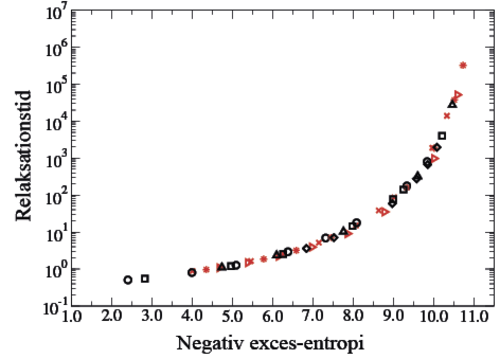
Figur 3: Figuren viser resultater fra studier af en væske-model ved omfattende computer-simuleringer. Man ser sammenhængen mellem relaksationstid (i et særligt enhedssystem) – det vil sige den tid, det tager for væsken at komme i ligevægt efter en ydre forstyrrelse – og exces-entropien, som er den entropi, der kun vedrører den potentielle energi.
De sorte symboler gælder for en større mængde væske ved forskellige tryk og temperaturer, mens de røde symboler er for den samme væske begrænset til en nano-kanal. Overraskende ser man, at der ingen forskel er! Figuren bekræfter og udvider “Rosenfelds exces-entropi skalering”, ifølge hvilken entropien bestemmer relaksationstiden.
Fra T. S. Ingebrigtsen, et al 2013
Fortsat plads til undren
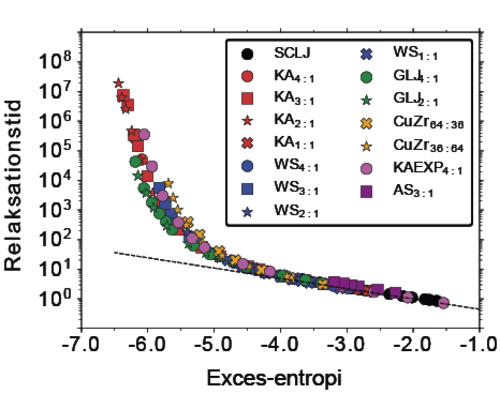
Da Rosenfeld gjorde sin opdagelse, var det på baggrund af studier af væsker med kun én type partikler, og han havde i øvrigt i 1977 slet ikke adgang til de hurtige computere, man råder over i dag. Vi har i Glas og Tid centeret på RUC computere baseret på grafik-kort (som oprindeligt er udviklet til spil) og råder over en regnekapacitet på godt 1000 Tera-flop, det vil sige 1015 regneoperationer per sekund. Vores computer-simuleringer har bekræftet Rosenfelds opdagelse, men også vist, at denne gælder mere generelt, end man hidtil har troet. Således er sammenhængen mellem exces-entropi og relaksationstid/viskositet den samme for en væske-model, uafhængigt af om væsken begrænses af en rand i kanaler af nanostørrelse eller ej (figur 3). Exces-entropien bestemmer også relaksationstiden for en række blandingsvæsker, oven i købet på en næsten universel måde (figur 4). Begge dele er overraskende og ikke fuldt ud forstået teoretisk selvom den såkaldte “isomorf-teori” udviklet på RUC giver en delvis forklaring.
Vi synes, det er spændende, at man fortsat kan undre sig over et helt grundlæggende begreb som entropi. Med denne artikel håber vi om ikke andet at have “forvirret læseren på et højere niveau”.
At entropien af et isoleret system ikke kan aftage opfattes inden for naturvidenskaben som en fundamental naturlov, og det er den naturlov, der ligger bag det faktum, at verden fremtræder irreversibel for os. Men entropien kan faktisk godt aftage en lille smule som en kort fluktuation – det er bare utroligt svært at måle. Loven om entropiens vækst er en pragmatisk sandhed, ikke en ontologisk sandhed. Om det samme er tilfældet for andre fundamentale naturlove, eller om entropiens lov har særstatus rent erkendelsesteoretisk, er et yderst interessant filosofisk spørgsmål. ♦