Igennem corona-krisen har vi ofte hørt om mørketal. Det henviser til alle de mennesker, der har været smittet med COVID-19, men som ikke optræder i statistikkerne, fordi de aldrig er testet positive - blandt andet på grund af manglen på testkapacitet i starten, eller fordi de ikke har haft symptomer. Vi ved derfor ikke, hvor stor en andel af befolkningen, der reelt har haft COVID-19, og derfor kan antages at være immune – det er et mørketal.

Hvorfor er det så vigtigt at kende mørketallet?

Fra en samfundsmæssig synsvinkel vil vi gerne kunne forudsige, hvor mange syge vi kan forvente i den kommende tid, og da er mørketallet vigtigt, fordi jo større andel af befolkningen, der er immune og ikke kan smitte videre, jo mindre spredning vil der være af sygdommen. Men også fra et personligt synspunkt vil vi gerne vide, om vi er immune og derfor ikke risikerer at blive syge eller at smitte andre.

Det viser sig imidlertid, at selvom vi kan lave pålidelige befolkningsundersøgelser, der kan estimere mørketallet, er det meget sværere at estimere nøjagtigt, hvem de immune personer er. Det skyldes en kontraintuitiv effekt, når små sandsynligheder er i spil, der kan være svær at forstå. Denne artikel handler om disse sandsynligheder, og hvordan de spiller sammen.

Krav til en god antistoftest

Det er ikke kun mørketallet, vi ikke kender. Der er stadig mange ting, vi ikke ved om COVID-19. Vi ved for eksempel ikke, om man bliver immun, og i så fald, hvor længe man er immun. Der er rapporteret få tilfælde af personer, der er testet positiv for COVID-19 to gange. Men det skal det ikke handle om her.

Lad os for nu antage, at man bliver immun, i hvert fald for en tid, og vi derfor kan bruge mørketallet til at forudsige udviklingen i smitten i befolkningen. Statens Serum Institut har for nyligt igangsat et større studie af befolkningen i Danmark for at afdække mørketallet, Vi tester Danmark, hvor en halv million personer har fået tilbudt en antistoftest.

En COVID-19-antistoftest er en blodprøve, der kan påvise, om en person har antistoffer mod SARS-CoV-2, den virus, der giver COVID-19-infektion. Mange antistoftest er i øjeblikket under udvikling, og der er allerede mange gode test tilgængelige, hvor “god” betyder, at testen har en høj sensitivitet og en høj specificitet. Sensitivitet er sandsynligheden for, at testen korrekt identificerer en person med antistoffer, også kendt som den sande positivrate.

En meget følsom test vil identificere de fleste mennesker, der har antistoffer, og kun en lille del af dem med antistoffer vil ikke blive fundet af testen, også kaldet falske negativer. Specificitet er sandsynligheden for, at testen korrekt identificerer en person uden antistoffer. Dette er kendt som den sande negativrate. En test med høj specificitet vil identificere de fleste mennesker uden antistoffer, og kun en lille del af dem uden antistoffer vil testen identificere som havende antistoffer, også kaldet falske positive.

Bemærk, at vi vil gerne have en test, hvor begge disse sandsynligheder er høje. Vi kan altid lave en test med 100% sensitivitet, hvis vi er ligeglade med specificiteten – vi kan jo bare sige, at alle er positive! Men det er åbenlyst ikke brugbart. Der er allerede udviklet flere test med en sensitivitet på næsten 100% og også en høj specificitet på omkring 95-99%. Med så store sandsynligheder må vi da kunne stole på resultatet af testen! Men, desværre, sådan er det ikke. Lad os se, hvorfor det ikke er tilfældet.

Når mørketallet spiller ind

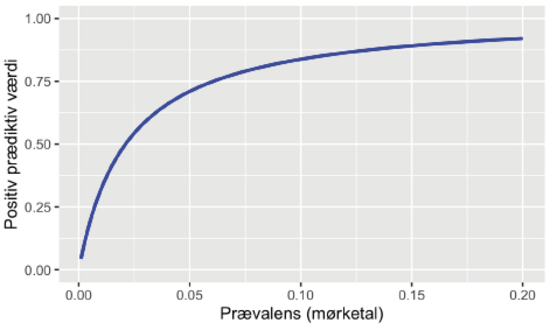
Sandsynligheden for, at personer med et positivt testresultat, virkelig har antistoffer kalder vi den positive prædiktive værdi. Det er altså den, vi er interesseret i, når vi bliver testet og vil vide, hvad sandsynligheden er for, at vi er immune, forudsat at testen er positiv. Men den positive prædiktive værdi er ikke det samme som sensitiviteten, og det er derfor, det er så vanskeligt. Mens sensitiviteten kun afhænger af egenskaber ved testen, afhænger den positive prædiktive værdi nemlig også af mørketallet – det vil sige andelen af befolkningen, der har antistoffer i blodet på tidspunktet for testen. Den positive prædiktive værdi vil typisk være meget mindre end sensitiviteten, hvis der ikke er så mange, der har antistoffer.

Sensitiviteten og den positive prædiktive værdi er kun de samme, hvis sandsynligheden for, at en person har antistoffer, er den samme som sandsynligheden for, at testen er positiv. Det kræver, at sensitiviteten og specificiteten er 100%, men det sker kun meget sjældent (hvis nogensinde!) for hvilken som helst test. Faktisk er de meget forskellige, hvis mørketallet er lavt, som det nok er de fleste steder på dette tidspunkt i pandemien. Det er nemlig sådan, at jo lavere mørketallet er, desto lavere er den positive prædiktive værdi. Det betyder, at en COVID-19-antistoftest, selv med høj sensitivitet og specificitet, der anvendes i områder, hvor mørketallet er lavt, vil have en lavere positiv prædiktiv værdi end i et område, hvor mørketallet er højere. Mørketallet varierer formentlig meget fra område til område, men de fleste steder i Danmark er et skøn på 2-5% nok ikke langt fra sandheden i skrivende stund.

Lad os antage en test med sensitivitet på 100% og specificitet på 98%, der bruges i et område, hvor mørketallet er 2%. Så er den positive prædiktive værdi lig med 0,5 (se sidste faktaboks). Selv med så god en test er sandsynligheden for at have haft COVID-19 altså kun fifty-fifty, selvom du tester positiv for antistoffer!

Usandsynlige hændelser i spil

Årsagen er, at der er to usandsynlige hændelser i spil: sandsynligheden for, at du er immun (en lille sandsynlighed givet ved mørketallet), og derfor testes positiv (med stor sandsynlighed, i eksemplet ovenfor med sandsynlighed en) – eller sandsynligheden for, at du vil blive testet positiv, selvom du ikke har antistoffer (en lille sandsynlighed), men mange mennesker uden antistoffer vil blive testet (fordi mørketallet er lille), og dermed vil antallet af falsk positive være stort.

Hvorfor dette er så kontraintuitivt forklares smukt i den stærkt anbefalelsesværdige bog af nobelprisvinder Daniel Kahneman, Thinking, Fast and Slow, der viser, hvordan vi psykologisk har tendens til at glemme eller ignorere forekomsten af det, vi undersøger (mørketallet) i lyset af yderligere information (resultatet af testen).

En lav positiv prædiktiv værdi betyder, at flere individer får et falsk positivt resultat, hvilket er farligt, da et positivt testresultat sandsynligvis vil gøre os mere afslappede og måske ændre adfærd, fordi vi ikke er bange for at blive smittet eller at smitte andre. I dette specielle eksempel kan vi være sikre på, at vi ikke har antistoffer, hvis vi får et negativt resultat, da sensitiviteten er 100%, så der er ingen falske negativer.

Et aktuelt eksempel

Lad os lave udregningerne for den antistoftest, der er blevet tilbudt et stort udsnit af den danske befolkning i kampagnen Vi tester Danmark. Her er sensitiviteten omkring 93% og specificiteten 98%. Testen er altså ikke lige så god som de bedste test, man kan få. Hvis mørketallet er 2%, da bliver den positive prædiktive værdi lig med 0,49. Det gør altså ikke den store forskel for den positive prædiktive værdi, at sensitiviteten er så meget lavere. Det er fordi, den største fejlkilde er falsk positive (og ikke falsk negative).

Formentlig er mørketallet højere visse steder, for eksempel i København, og det gør faktisk en stor forskel. Lad os antage, at den er 5%, da får vi, at den positive prædiktive værdi er lig med 0,71. Den positive prædiktive værdi stiger altså fra omkring 50% til omkring 70%, blot fordi mørketallet stiger fra 2 til 5%.

Selvom det er svært at identificere de specifikke personer, der har antistoffer, kan vi stadig bruge testene til at opnå gode estimater af mørketallet. Hvis vi tester mange, kan vi korrigere for det forventede antal falske positive og falske negativer. Vi kan derfor få rimelige befolkningsestimater, selvom de individuelle estimater ikke er gode.  ♦